



Next: Characterization of extracted Spectra
Up: Correction of Spectra for
Previous: The Location of Spectra
The functional form of the relation between the intra-pixel position
and quantum efficiency depends on detector properties, the point
spread function and the size of the imaged object. For point sources,
the function can be determined empirically. It is easy to formulate the
problem in terms of a correction factor fl to the
extracted spectrum, where the true spectrum 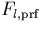 relates to the
raw extracted spectrum Fl as
relates to the
raw extracted spectrum Fl as
| 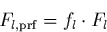 |
(23) |
where l labels the different wavelength bins. For simplicity, the dispersion
relation here is assumed to be linear,
| 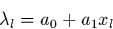 |
(24) |
where xl is the deflection of the lth wavelength bin in pixels
relative to the position of the object on the direct image. A simple
model for the correction factor was fitted to the calibration data of
the first NICMOS campaign,
| ![\begin{displaymath}
f_l(\lambda)= 1 + A \cos [p (\lambda-a_0) + \psi]\end{displaymath}](img69.gif) |
(25) |
The period p is given by
| 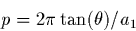 |
(26) |
where a1 is the dispersion in 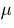 /pixel, and the
phase
/pixel, and the
phase 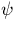 by
by
| 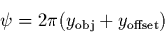 |
(27) |
where 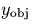 is the position of the object on the direct image,
and
is the position of the object on the direct image,
and 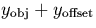 is the y coordinate of the
spectrum at the reference wavelength a0. For high signal-to-noise
spectra,
is the y coordinate of the
spectrum at the reference wavelength a0. For high signal-to-noise
spectra, 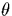 and
and 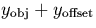 can easily be
determined. The only free parameter to be directly determined from
the extracted calibration spectra is the amplitude
A. Figure 3.16 shows the fit to the calibration data taken
during the first NICMOS campaign. The amplitudes determined from
NICMOS campaigns (when NIC3 was in focus) is about 0.1, whereas
outside the campaigns the amplitudes are about 0.05. Significant
deviations from these average values have been detected, and it is
currently not known whether these changes in amplitude correspond to
changes in the PSF or are due to the calibration data taken at
different positions on the detectors. Because of these variations in
amplitude, we estimate that correction for PRF will on average reduce
the amplitude of the wave like pattern in spectra by a factor of 2 to
5.
can easily be
determined. The only free parameter to be directly determined from
the extracted calibration spectra is the amplitude
A. Figure 3.16 shows the fit to the calibration data taken
during the first NICMOS campaign. The amplitudes determined from
NICMOS campaigns (when NIC3 was in focus) is about 0.1, whereas
outside the campaigns the amplitudes are about 0.05. Significant
deviations from these average values have been detected, and it is
currently not known whether these changes in amplitude correspond to
changes in the PSF or are due to the calibration data taken at
different positions on the detectors. Because of these variations in
amplitude, we estimate that correction for PRF will on average reduce
the amplitude of the wave like pattern in spectra by a factor of 2 to
5.
Figure 3.16:
Fit of the PRF correction factor. The data are the same
as in figure 3.14 and 3.15. With the amplitude
A as the only free parameter, the behavior of both grisms can be fitted
with the model. Note in particular that the amplitude seems to be almost
independent of wavelength.
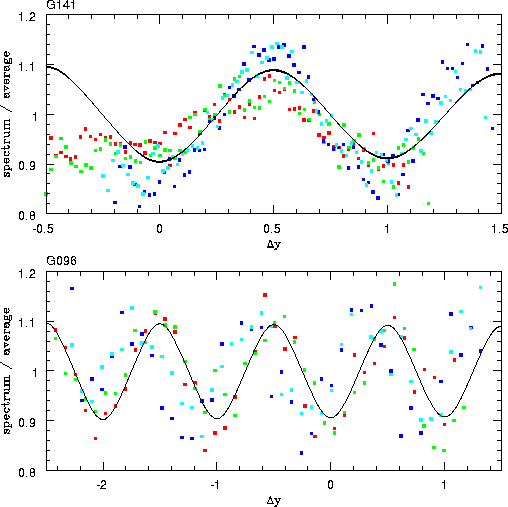 |




Next: Characterization of extracted Spectra
Up: Correction of Spectra for
Previous: The Location of Spectra
Wolfram Freudling
5/29/1999
![]() relates to the
raw extracted spectrum Fl as
relates to the
raw extracted spectrum Fl as
![]() is the position of the object on the direct image,
and
is the position of the object on the direct image,
and ![]() is the y coordinate of the
spectrum at the reference wavelength a0. For high signal-to-noise
spectra,
is the y coordinate of the
spectrum at the reference wavelength a0. For high signal-to-noise
spectra, ![]() and
and ![]() can easily be
determined. The only free parameter to be directly determined from
the extracted calibration spectra is the amplitude
A. Figure 3.16 shows the fit to the calibration data taken
during the first NICMOS campaign. The amplitudes determined from
NICMOS campaigns (when NIC3 was in focus) is about 0.1, whereas
outside the campaigns the amplitudes are about 0.05. Significant
deviations from these average values have been detected, and it is
currently not known whether these changes in amplitude correspond to
changes in the PSF or are due to the calibration data taken at
different positions on the detectors. Because of these variations in
amplitude, we estimate that correction for PRF will on average reduce
the amplitude of the wave like pattern in spectra by a factor of 2 to
5.
can easily be
determined. The only free parameter to be directly determined from
the extracted calibration spectra is the amplitude
A. Figure 3.16 shows the fit to the calibration data taken
during the first NICMOS campaign. The amplitudes determined from
NICMOS campaigns (when NIC3 was in focus) is about 0.1, whereas
outside the campaigns the amplitudes are about 0.05. Significant
deviations from these average values have been detected, and it is
currently not known whether these changes in amplitude correspond to
changes in the PSF or are due to the calibration data taken at
different positions on the detectors. Because of these variations in
amplitude, we estimate that correction for PRF will on average reduce
the amplitude of the wave like pattern in spectra by a factor of 2 to
5.
