The Location of Spectra and the Response Function

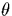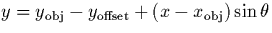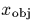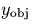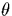Spectra on NICMOS grism images are not exactly aligned with the row of the images. Therefore, different parts of a spectrum fall at different y-locations (see figure 3.11). If distortions in the spectra are neglected, the y-position of a spectrum as a function of its x position for a given inclination $\theta$ can be written as $y= y_{\rm obj} - y_{\rm offset} + (x-x_{\rm obj}) \sin \theta$ , where $x_{\rm obj}$ and $y_{\rm obj}$ are the coordinates of the spectrum on the direct image, and $y_{\rm offset}$ is the offset between the grism and direct image. The x position of the spectrum corresponds to the wavelength of the extracted spectrum. Therefore, a non-zero $\theta$ implies that at some wavelength, the spectrum is located between two rows on the detector, while at other wavelengths, the spectrum is centered on a particular row.

**Figure 3.11:** Schematic of the spectrum location as a function of x-coordinate. The spectrum is inclined relative to the rows of the detector by an angle 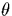$\theta$ . This inclination puts the center of the spectrum at different y-locations as a function of wavelength. The spectrum is at the center of a row at the indicated positions, which correspond to different wavelength wavelengths. 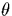A change of $\theta$ or and overall shift of the spectrum along the y-axis by a fraction of a pixel will change the wavelength at which the centers of rows are crossed.
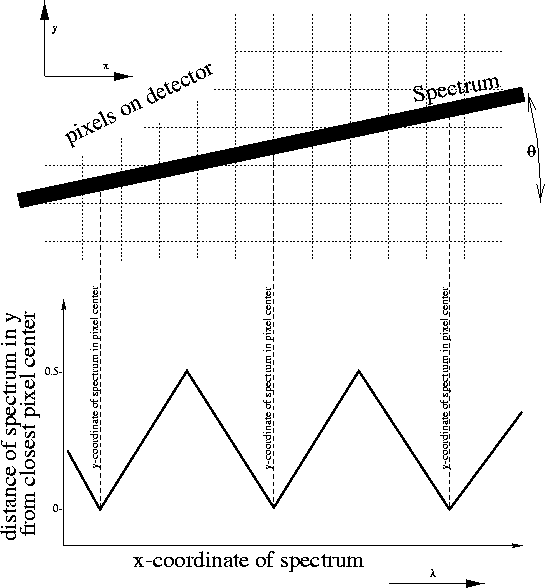$\begin{figure} \psfig {figure=figs/cartoon.eps,width=12cm} \end{figure}$

**Figure 3.12:** Measured raw magnitudes of a star in the HDF-S field. The magnitude of the same star has been measured on individual exposures, which were taken at different dither positions. The magnitudes are plotted as a function of the measured position of the star relative to the closest pixel center. The data were kindly provided by Richard Hook.
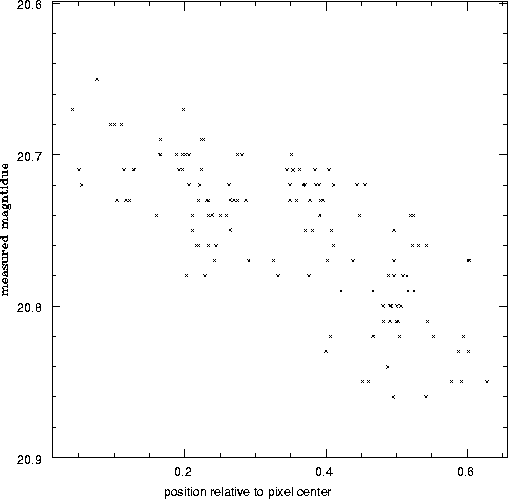$\begin{figure} \psfig {figure=figs/hdf_subpix.eps,width=12cm} \end{figure}$

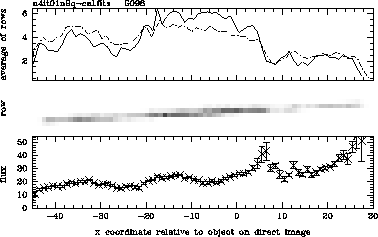
**Figure 3.13:** A NICMOS Grism spectrum of the flux calibrator P330e. The middle panel shows a cutout from the NICMOS grism images. Wavelength decreases to the right. Note that at any wavelength, most of the flux is contained in one or two pixels. The regions where the spectrum lies between two rows can easily be identified. At these places, the flux in the spectrum seem to be below the flux in adjacent regions in the spectrum. This visual impression is strengthened by the plot in the upper panel, which shows the average of each column in the cut out as a function of x coordinates relative to the position of the object on the grism image. Finally, the lower panel shows a spectrum extracted by NICMOSlook with the PRF correction option turned off. The x-axes of all three panels are aligned. Comparison of the upper and lower panels show that the flux calibration of NICMOSlook correctly converts the raw fluxes into the expected overall shape of the spectrum. However, the flux is underestimated where the spectrum crosses the boundary between rows.
$\begin{figure} \vskip6.0truecm\special{psfile=figs/effect_demo.ps voffset=30cm}\end{figure}$

The quantum efficiency (QE) of NICMOS depends on the exact position within each pixel where the photon hits the detector. The effect of this intra-pixel response function (PRF)on the photometry of point sources is shown in figure 3.12. A similar impact is expected on the flux calibration of extracted spectra of point sources. The flux in each wavelength bin of a spectrum is similar the aperture magnitude measured in point source photometry. The inclination of the spectrum relative to the rows implies that the quantum efficiency and therefore the flux calibration of spectra is a function of the intra pixel position of the object. This is shown in Figure 3.13, which shows a grism image and extracted spectra of a calibrator source. The spectrum is modulated by a wave-like pattern. The phase of this pattern is determined by the fact that the QE is at its minimum where the spectrum falls between two rows.

**Figure 3.14:** Four spectra of calibrator P330e taken with grism G141. The four spectra were placed at different dither positions, which resulted in different sub-pixel locations of the object. The upper panel shows the spectra as extracted by NICMOSlook, divided by a model of the spectrum of the star. It can be seen that the different extracted spectra deviate in a wave-like pattern with an amplitude of about 10% from the average spectrum. The lower panel shows the same data plotted as a function of 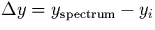$\Delta y= y_{\rm spectrum}-y_i$ , where y is the row of the spectrum location, and y_i is an arbitrary integer number chosen separately for each spectrum. It can be seen that the imprinted pattern of the individual spectra are now shifted and are in phase. This demonstrates that the phase of the pattern is determined by the intra-pixel position of the spectrum.
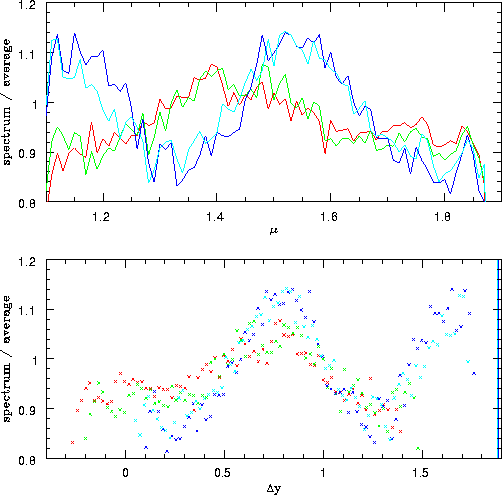$\begin{figure} \psfig {figure=figs/spec_g141_2.ps,width=12cm} \end{figure}$

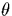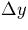**Figure 3.15:** Same plot as figure 3.14, but for grism G096. The inclination $\theta$ of G096 is larger than the one of G141. This is the reason for the larger range of $\Delta y$ covered. In the spectrum, this will show as a shorter period of the PRF pattern in the spectrum.
$\begin{figure} \psfig {figure=figs/spec_g096_2.ps,width=12cm} \end{figure}$

The effect on the flux calibration is shown in figures 3.14 and 3.15. The figures show extracted spectra of a calibration source extracted from dithered exposures which lead to different sub-pixel y-coordinates of the star. It can be seen that the amplitude of the wave-like pattern imprinted on the spectra is about 10%, the period is determined by the inclination of the spectrum relative to the rows of the detector, and the phase is determined by the intra-pixel position of the spectrum.