Correction for Contamination

From the contamination factors, the spectra can be corrected. The crucial simplifying assumption is that the spectrum of every object is independent of the position within the object. In that case, for a given wavelength in one spectrum, the contamination can simply be written as a set of linear equations,

$$\vec{F}_{meas} = M \cdot \vec{F}_{true}$$ (17)

where $\vec{F}_{meas}$ is a vector of fluxes for a set of contaminating objects as extracted from the grism image. The ith element of the vector contains the flux from object i at a wavelength which contaminates the wavelength of object j. $\vec{F}_{meas}$ is the equivalent vector as it would be measured if all the spectra were isolated from each other.

The matrix M contains in the i-th column of row j the contamination of spectrum i from spectrum j. If there is no contamination, there would be a zero. This matrix has a "1" in the diagonal (i.e. for i=j), which means just that we assume that the spectrum i contains all the flux from object i, and, in addition, the contamination from other spectra.

Figure 3.5 shows two simple examples which can be treated by this algorithm. In both examples, at least part of one spectrum is not contaminated. Since the underlying assumption is that the contaminated parts of the spectra have the same features as the uncontaminated parts, this information can be used to deduce each spectrum. This is accomplished by solving equation 3.19 by simply inverting the matrix. After computing the inverted matrix I with matrix elements I_i,j, we can compute the corrected ("true") spectra for each wavelength:

$$\vec{F}_{true}= I \cdot \vec{F}_{meas}$$ (18)

or

 

$$F_{true,i} = \sum_{j=1,n_{ov}} ( I_{i,j} F_{meas,j} )$$ (19)

where n_ov is the number of overlapping spectra at this wavelength.

Note that in general the situation could be more complex than those shown in figure 3.5. At a given wavelength, spectrum i could be contaminated by spectrum j and k, and spectrum k itself could be contaminated by another spectrum l (in addition to spectrum i, of course). This situation is illustrated in figure 3.6. In this case, n_ov=4 and the set of linear equations would be:

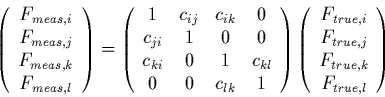$$\left(\begin{array} {c} F_{meas,i} \\ F_{meas,j} \\ F_{meas,... ...} \\ F_{true,j} \\ F_{true,k} \\ F_{true,l}\end{array} \right)$$ (20)

Note that c_ji is not necessarily the same as c_ij. The contamination of spectrum i from spectrum j is not necessarily the same as the contamination of spectrum j from i.