



Next: Response Files
Up: Flux Calibration
Previous: Flux Calibration
Once a spectrum has been extracted, it is flux calibrated by
dividing it by the grism response function pointed to in the
$CALNICC_BASE/calib/grismspec.dat file. The calibrated spectrum
is computed as
| 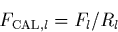 |
(7) |
where Rl is the response for the lth wavelength bin.
This flux calibration introduces additional uncertainties in the
extracted spectra. An error 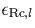 is attached to
each flux calibration value Rl. In addition, the uncertainty in the
zero point of the wavelength calibration due to errors in the
measurements of the object x coordinate leads to an error in the applied
response at a particular wavelength. This uncertainty is estimated as
is attached to
each flux calibration value Rl. In addition, the uncertainty in the
zero point of the wavelength calibration due to errors in the
measurements of the object x coordinate leads to an error in the applied
response at a particular wavelength. This uncertainty is estimated as
| 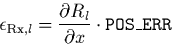 |
(8) |
where POS_ERR is the uncertainty of the zero point of
wavelength calibration in pixels, i.e. the uncertainty of the x
position of the object on the direct image. POS_ERR is a user
supplied parameter. Realistic values are on the order of 0.5
pixels. The total error in the flux calibration is
| 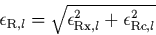 |
(9) |
This error has to be taken into account in the estimate of the total
uncertainty of an extracted spectrum (see section 3.5.7).




Next: Response Files
Up: Flux Calibration
Previous: Flux Calibration
Wolfram Freudling
5/29/1999
![]() is attached to
each flux calibration value Rl. In addition, the uncertainty in the
zero point of the wavelength calibration due to errors in the
measurements of the object x coordinate leads to an error in the applied
response at a particular wavelength. This uncertainty is estimated as
is attached to
each flux calibration value Rl. In addition, the uncertainty in the
zero point of the wavelength calibration due to errors in the
measurements of the object x coordinate leads to an error in the applied
response at a particular wavelength. This uncertainty is estimated as